En general vamos a trabajar con las ecuaciones de Einstein acopladas con un campo escalar como fuente. En el límite Newtoniano, estas ecuaciones se reducen a las ecuaciones de Schroedinger-Poisson, estas son:

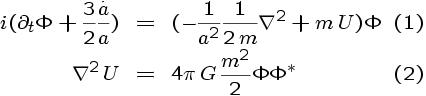
En donde a es el factor de escala del universo, m la masa del campo escalar, U el potencial Newtoniano, G la constante de Newton y el campo escalar. El punto significa derivada con respecto al tiempo y * complejo conjugado. Nosotros no vamos a ser los primeros en estudiar el sistema (1),(2), pero si los primeros en hacerlo con un propósito astrofísico de esta naturaleza.
Para poder estudiar el colapso de un campo escalar sin simetría esférica, es necesario tomar varios pasos. Lo primero que estamos haciendo es escribir un código en una aproximación Newtoniana, para un colapso axial simétrico. Este código es mucho más simple de elaborar y nos dará una idea de que tenemos que esperar con un colapso relativista. El segundo paso es hacer el mismo código, pero relativista, el cual es ya mucho más elaborado. En este caso hay que resolver la ecuación

Gab = k Tab

Donde Gab es el tensor de Einstein y Tab es el tensor de Energia Materia del campo escalar:

Estos dos códigos nos darán las bases para el trabajo siguiente, que es un código sin simetrías. De nuevo, la táctica es primero hacer un código Newtoniano y luego un código relativista. Este último código será de un alto grado de dificultad, ya que contiene todos los términos de las ecuaciones de Einstein. Afortunadamente no esperamos tener singularidades en el colapso, por lo que los problemas con horizontes están descartados.

Para la paralización de los códigos, pensamos usar el paquete computacional llamado Cactus, que es un paquete ya paralelizado y que funciona muy bien. Es gratis y varios de los colaboradores ya lo saben usar. Las corridas se harán en el cluster del Cinvestav, que ya esta funcionando desde mediados del 2005.