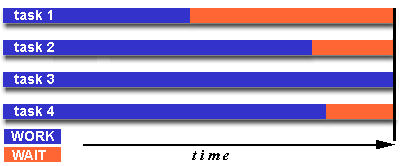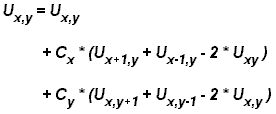|
Introduction to Parallel Computing
| |
Table of Contents
- Abstract
- Overview
- What is
Parallel Computing?
- Why Use
Parallel Computing?
- Concepts
and Terminology
- von
Neumann Computer Architecture
- Flynn's
Classical Taxonomy
- Some
General Parallel Terminology
- Parallel
Computer Memory Architectures
- Shared
Memory
- Distributed
Memory
- Hybrid
Distributed-Shared Memory
- Parallel
Programming Models
- Overview
- Shared
Memory Model
- Threads
Model
- Message
Passing Model
- Data
Parallel Model
- Other
Models
- Designing
Parallel Programs
- Automatic
vs. Manual Parallelization
- Understand
the Problem and the Program
- Partitioning
- Communications
- Synchronization
- Data
Dependencies
- Load
Balancing
- Granularity
- I/O
- Limits
and Costs of Parallel Programming
- Performance
Analysis and Tuning
- Parallel
Examples
- Array
Processing
- PI
Calculation
- Simple
Heat Equation
- 1-D
Wave Equation
- References
and More Information
This presentation covers the basics of parallel computing. Beginning with
a brief overview and some concepts and terminology associated with parallel
computing, the topics of parallel memory architectures and programming models
are then explored. These topics are followed by a discussion on a number of
issues related to designing parallel programs. The last portion of the
presentation is spent examining how to parallelize several different types of
serial programs.
Level/Prerequisites: None
What is Parallel Computing?
- Traditionally, software has been written for serial
computation:
- To be executed by a single computer having a single Central Processing
Unit (CPU);
- Problems are solved by a series of instructions, executed one after the
other by the CPU. Only one instruction may be executed at any moment in
time.
- In the simplest sense, parallel computing is the
simultaneous use of multiple compute resources to solve a computational
problem.
- The compute resources can include:
- A single computer with multiple processors;
- An arbitrary number of computers connected by a network;
- A combination of both.
- The computational problem usually demonstrates characteristics such as the
ability to be:
- Broken apart into discrete pieces of work that can be solved
simultaneously;
- Execute multiple program instructions at any moment in time;
- Solved in less time with multiple compute resources than with a single
compute resource.
- Parallel computing is an evolution of serial computing that attempts to
emulate what has always been the state of affairs in the natural world: many
complex, interrelated events happening at the same time, yet within a
sequence. Some examples:
- Planetary and galactic orbits
- Weather and ocean patterns
- Tectonic plate drift
- Rush hour traffic in LA
- Automobile assembly line
- Daily operations within a business
- Building a shopping mall
- Ordering a hamburger at the drive through.
- Traditionally, parallel computing has been considered to be "the high end
of computing" and has been motivated by numerical simulations of complex
systems and "Grand Challenge Problems" such as:
- weather and climate
- chemical and nuclear reactions
- biological, human genome
- geological, seismic activity
- mechanical devices - from prosthetics to spacecraft
- electronic circuits
- manufacturing processes
- Today, commercial applications are providing an equal or greater driving
force in the development of faster computers. These applications require the
processing of large amounts of data in sophisticated ways. Example
applications include:
- parallel databases, data mining
- oil exploration
- web search engines, web based business services
- computer-aided diagnosis in medicine
- management of national and multi-national corporations
- advanced graphics and virtual reality, particularly in the entertainment
industry
- networked video and multi-media technologies
- collaborative work environments
- Ultimately, parallel computing is an attempt to maximize the infinite but
seemingly scarce commodity called time.
Why Use Parallel Computing?
- There are two primary reasons for using parallel computing:
- Save time - wall clock time
- Solve larger problems
- Other reasons might include:
- Taking advantage of non-local resources - using available compute
resources on a wide area network, or even the Internet when local compute
resources are scarce.
- Cost savings - using multiple "cheap" computing resources instead of
paying for time on a supercomputer.
- Overcoming memory constraints - single computers have very finite memory
resources. For large problems, using the memories of multiple computers may
overcome this obstacle.
- Limits to serial computing - both physical and practical reasons pose
significant constraints to simply building ever faster serial computers:
- Transmission speeds - the speed of a serial computer is directly
dependent upon how fast data can move through hardware. Absolute limits are
the speed of light (30 cm/nanosecond) and the transmission limit of copper
wire (9 cm/nanosecond). Increasing speeds necessitate increasing proximity
of processing elements.
- Limits to miniaturization - processor technology is allowing an
increasing number of transistors to be placed on a chip. However, even with
molecular or atomic-level components, a limit will be reached on how small
components can be.
- Economic limitations - it is increasingly expensive to make a single
processor faster. Using a larger number of moderately fast commodity
processors to achieve the same (or better) performance is less expensive.
- The future: during the past 10 years, the trends indicated by ever faster
networks, distributed systems, and multi-processor computer architectures
(even at the desktop level) suggest that parallelism is the future of
computing.
von Neumann Architecture
- For over 40 years, virtually all computers have followed a common machine
model known as the von Neumann computer. Named after the Hungarian
mathematician John von Neumann.
- A von Neumann computer uses the stored-program concept. The CPU executes a
stored program that specifies a sequence of read and write operations on the
memory.
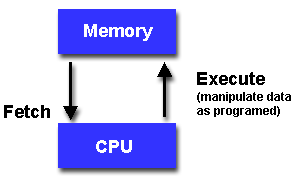
- Basic design:
- Memory is used to store both program and data instructions
- Program instructions are coded data which tell the computer to do
something
- Data is simply information to be used by the program
- A central processing unit (CPU) gets instructions and/or data from
memory, decodes the instructions and then sequentially
performs them.
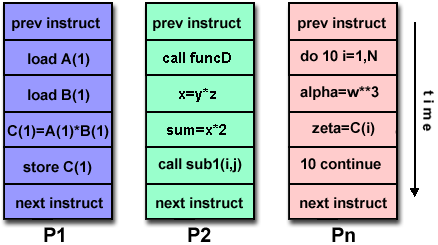
Flynn's Classical Taxonomy
- There are different ways to classify parallel computers. One of the more
widely used classifications, in use since 1966, is called Flynn's Taxonomy.
- Flynn's taxonomy distinguishes multi-processor computer architectures
according to how they can be classified along the two independent dimensions
of Instruction and Data. Each of these dimensions
can have only one of two possible states: Single or
Multiple.
- The matrix below defines the 4 possible classifications according to
Flynn.
S I S D
Single Instruction, Single Data |
S I M D
Single Instruction, Multiple Data |
M I S D
Multiple Instruction, Single Data |
M I M D
Multiple Instruction, Multiple
Data |
 Single Instruction, Single Data
(SISD): Single Instruction, Single Data
(SISD):
- A serial (non-parallel) computer
- Single instruction: only one instruction stream is being acted on by
the CPU during any one clock cycle
- Single data: only one data stream is being used as input during any
one clock cycle
- Deterministic execution
- This is the oldest and until recently, the most prevalent form of
computer
- Examples: most PCs, single CPU workstations and mainframes
|
 |
 Single Instruction, Multiple Data
(SIMD): Single Instruction, Multiple Data
(SIMD):
- A type of parallel computer
- Single instruction: All processing units execute the same
instruction at any given clock cycle
- Multiple data: Each processing unit can operate on a different data
element
- This type of machine typically has an instruction dispatcher, a very
high-bandwidth internal network, and a very large array of very
small-capacity instruction units.
- Best suited for specialized problems characterized by a high degree
of regularity,such as image processing.
- Synchronous (lockstep) and deterministic execution
- Two varieties: Processor Arrays and Vector Pipelines
- Examples (some extinct):
- Processor Arrays: Connection Machine CM-2, Maspar MP-1, MP-2
- Vector Pipelines: IBM 9000, Cray C90, Fujitsu VP, NEC SX-2,
Hitachi S820
|
 |
 Multiple Instruction, Single Data (MISD):
Multiple Instruction, Single Data (MISD):
- Few actual examples of this class of parallel computer have ever existed
- Some conceivable examples might be:
- multiple frequency filters operating on a single signal stream
- multiple cryptography algorithms attempting to crack a single coded
message.
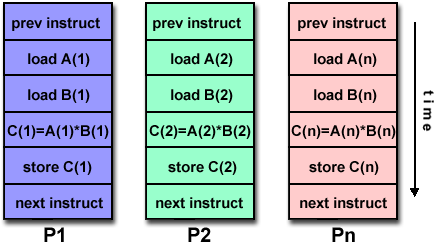
 Multiple Instruction, Multiple Data
(MIMD): Multiple Instruction, Multiple Data
(MIMD):
- Currently, the most common type of parallel computer
- Multiple Instruction: every processor may be executing a different
instruction stream
- Multiple Data: every processor may be working with a different data
stream
- Execution can be synchronous or asynchronous, deterministic or non-
deterministic
- Examples: most current supercomputers, networked parallel computer
"grids" and multi-processor SMP computers - including some types of PCs.
|
 |
Some General Parallel Terminology
Like everything else, parallel
computing has its own "jargon". Some of the more commonly used terms associated
with parallel computing are listed below.
- Task
- A logically discrete section of computational work. A task is typically a
program or program-like set of instructions that is executed by a processor.
- Parallel Task
- A task that can be executed by multiple processors safely (yields correct
results)
- Serial Execution
- Execution of a program sequentially, one statement at a time. In the
simplest sense, this is what happens on a one processor machine. However,
virtually all parallel tasks will have sections of a parallel program that
must be executed serially.
- Parallel Execution
- Execution of a program by more than one task, with each task being able to
execute the same or different statement at the same moment in time.
- Shared Memory
- From a strictly hardware point of view, describes a computer architecture
where all processors have direct (usually bus based) access to common physical
memory. In a programming sense, it describes a model where parallel tasks all
have the same "picture" of memory and can directly address and access the same
logical memory locations regardless of where the physical memory actually
exists.
- Distributed Memory
- In hardware, refers to network based memory access for physical memory
that is not common. As a programming model, tasks can only logically "see"
local machine memory and must use communications to access memory on other
machines where other tasks are executing.
- Communications
- Parallel tasks typically need to exchange data. There are several ways
this can be accomplished, such as through a shared memory bus or over a
network, however the actual event of data exchange is commonly referred to as
communications regardless of the method employed.
- Synchronization
- The coordination of parallel tasks in real time, very often associated
with communications. Often implemented by establishing a synchronization point
within an application where a task may not proceed further until another
task(s) reaches the same or logically equivalent point.
Synchronization usually involves waiting by at least one task, and can
therefore cause a parallel application's wall clock execution time to
increase.
- Granularity
- In parallel computing, granularity is a qualitative measure of the ratio
of computation to communication.
- Coarse: relatively large amounts of computational work are
done between communication events
- Fine: relatively small amounts of computational work are
done between communication events
- Observed Speedup
- Observed speedup of a code which has been parallelized, defined as:
wall-clock time of serial execution
wall-clock time of parallel execution |
One of the simplest and most widely used indicators for a parallel
program's performance.
- Parallel Overhead
- The amount of time required to coordinate parallel tasks, as opposed to
doing useful work. Parallel overhead can include factors such as:
- Task start-up time
- Synchronizations
- Data communications
- Software overhead imposed by parallel compilers, libraries, tools,
operating system, etc.
- Task termination time
- Massively Parallel
- Refers to the hardware that comprises a given parallel system - having
many processors. The meaning of many keeps increasing, but currently means
more than 1000.
- Scalability
- Refers to a parallel system's (hardware and/or software) ability to
demonstrate a proportionate increase in parallel speedup with the addition of
more processors. Factors that contribute to scalability include:
- Hardware - particularly memory-cpu bandwidths and network communications
- Application algorithm
- Parallel overhead related
- Characteristics of your specific application and coding
| Parallel Computer Memory
Architectures |
Shared Memory
 General Characteristics:
General Characteristics:
- Shared memory parallel computers vary widely, but generally have in common
the ability for all processors to access all memory as global address space.
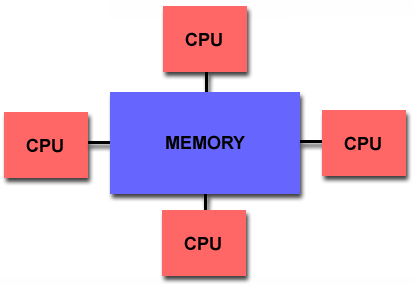
- Multiple processors can operate independently but share the same memory
resources.
- Changes in a memory location effected by one processor are visible to all
other processors.
- Shared memory machines can be divided into two main classes based upon
memory access times: UMA and NUMA.
 Uniform Memory Access (UMA):
Uniform Memory Access (UMA):
- Most commonly represented today by Symmetric Multiprocessor (SMP) machines
- Identical processors
- Equal access and access times to memory
- Sometimes called CC-UMA - Cache Coherent UMA. Cache coherent means if one
processor updates a location in shared memory, all the other processors know
about the update. Cache coherency is accomplished at the hardware level.
 Non-Uniform Memory Access (NUMA):
Non-Uniform Memory Access (NUMA):
- Often made by physically linking two or more SMPs
- One SMP can directly access memory of another SMP
- Not all processors have equal access time to all memories
- Memory access across link is slower
- If cache coherency is maintained, then may also be called CC-NUMA - Cache
Coherent NUMA
 Advantages:
Advantages:
- Global address space provides a user-friendly programming perspective to
memory
- Data sharing between tasks is both fast and uniform due to the proximity
of memory to CPUs
 Disadvantages:
Disadvantages:
- Primary disadvantage is the lack of scalability between memory and CPUs.
Adding more CPUs can geometrically increases traffic on the shared memory-CPU
path, and for cache coherent systems, geometrically increase traffic
associated with cache/memory management.
- Programmer responsibility for synchronization constructs that insure
"correct" access of global memory.
- Expense: it becomes increasingly difficult and expensive to design and
produce shared memory machines with ever increasing numbers of processors.
| Parallel Computer Memory
Architectures |
Distributed Memory
 General Characteristics:
General Characteristics:
- Like shared memory systems, distributed memory systems vary widely but
share a common characteristic. Distributed memory systems require a
communication network to connect inter-processor memory.
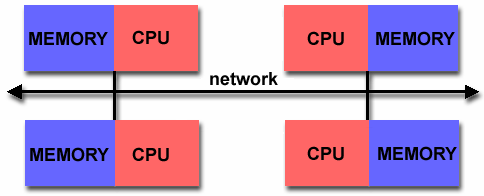
- Processors have their own local memory. Memory addresses in one processor
do not map to another processor, so there is no concept of global address
space across all processors.
- Because each processor has its own local memory, it operates
independently. Changes it makes to its local memory have no effect on the
memory of other processors. Hence, the concept of cache coherency does not
apply.
- When a processor needs access to data in another processor, it is usually
the task of the programmer to explicitly define how and when data is
communicated. Synchronization between tasks is likewise the programmer's
responsibility.
- The network "fabric" used for data transfer varies widely, though it can
can be as simple as Ethernet.
 Advantages:
Advantages:
- Memory is scalable with number of processors. Increase the number of
processors and the size of memory increases proportionately.
- Each processor can rapidly access its own memory without interference and
without the overhead incurred with trying to maintain cache coherency.
- Cost effectiveness: can use commodity, off-the-shelf processors and
networking.
 Disadvantages:
Disadvantages:
- The programmer is responsible for many of the details associated with data
communication between processors.
- It may be difficult to map existing data structures, based on global
memory, to this memory organization.
- Non-uniform memory access (NUMA) times
| Parallel Computer Memory
Architectures |
Hybrid Distributed-Shared Memory
- Summarizing a few of the key characteristics of shared and distributed
memory machines:
| Comparison of Shared and Distributed Memory
Architectures |
| Architecture |
CC-UMA |
CC-NUMA |
Distributed |
| Examples |
SMPs
Sun Vexx
DEC/Compaq
SGI Challenge
IBM POWER3 |
SGI Origin
Sequent
HP Exemplar
DEC/Compaq
IBM
POWER4 |
Cray T3E
Maspar
IBM SP2 |
| Communications |
MPI
Threads
OpenMP
shmem |
MPI
Threads
OpenMP
shmem |
MPI |
| Scalability |
to 10s of processors |
to 100s of processors |
to 1000s of processors |
| Draw Backs |
Memory-CPU bandwidth |
Memory-CPU bandwidth
Non-uniform access times |
System administration
Programming is hard to develop and
maintain |
| Software Availability |
many 1000s ISVs |
many 1000s ISVs |
100s ISVs |
- The largest and fastest computers in the world today employ both shared
and distributed memory architectures.
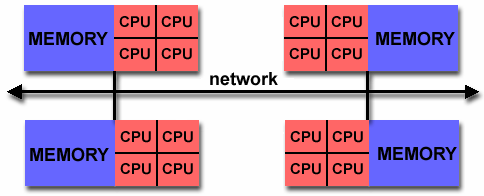
- The shared memory component is usually a cache coherent SMP machine.
Processors on a given SMP can address that machine's memory as global.
- The distributed memory component is the networking of multiple SMPs. SMPs
know only about their own memory - not the memory on another SMP. Therefore,
network communications are required to move data from one SMP to another.
- Current trends seem to indicate that this type of memory architecture will
continue to prevail and increase at the high end of computing for the
foreseeable future.
- Advantages and Disadvantages: whatever is common to both shared and
distributed memory architectures.
| Parallel Programming
Models |
Overview
- There are several parallel programming models in common use:
- Shared Memory
- Threads
- Message Passing
- Data Parallel
- Hybrid
- Parallel programming models exist as an abstraction above hardware and
memory architectures.
- Although it might not seem apparent, these models are NOT specific to a
particular type of machine or memory architecture. In fact, any of these
models can (theoretically) be implemented on any underlying hardware. Two
examples:
- Shared memory model on a distributed memory machine: Kendall Square
Research (KSR) ALLCACHE approach.
Machine memory was physically distributed, but appeared to the user as a
single shared memory (global address space). Generically, this approach is
referred to as "virtual shared memory". Note: although KSR is no longer in
business, there is no reason to suggest that a similar implementation will
not be made available by another vendor in the future.
- Message passing model on a shared memory machine: MPI on SGI Origin.
The SGI Origin employs the CC-NUMA type of shared memory architecture,
where every task has direct access to global memory. However, the ability to
send and receive messages with MPI, as is commonly done over a network of
distributed memory machines, is not only implemented but is very commonly
used.
- Which model to use is often a combination of what is available and
personal choice. There is no "best" model, although there certainly are better
implementations of some models over others.
- The following sections describe each of the models mentioned above, and
also discuss some of their actual implementations.
| Parallel Programming
Models |
Shared Memory Model
- In the shared-memory programming model, tasks share a common address
space, which they read and write asynchronously.
- Various mechanisms such as locks / semaphores may be used to control
access to the shared memory.
- An advantage of this model from the programmer's point of view is that the
notion of data "ownership" is lacking, so there is no need to specify
explicitly the communication of data between tasks. Program development can
often be simplified.
- An important disadvantage in terms of performance is that it becomes more
difficult to understand and manage data locality.
 Implementations:
Implementations:
- On shared memory platforms, the native compilers translate user program
variables into actual memory addresses, which are global.
- No common distributed memory platform implementations currently exist.
However, as mentioned previously in the Overview section, the KSR ALLCACHE
approach provided a shared memory view of data even though the physical memory
of the machine was distributed.
| Parallel Programming
Models |
Threads Model
- In the threads model of parallel programming, a single process can have
multiple, concurrent execution paths.
- Perhaps the most simple analogy that can be used to describe threads is
the concept of a single program that includes a number of subroutines:
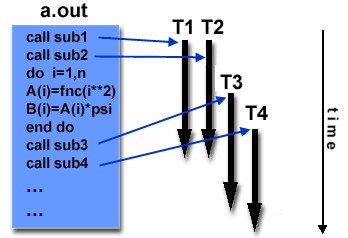
- The main program a.out is scheduled to run by the native
operating system. a.out loads and acquires all of the necessary
system and user resources to run.
- a.out performs some serial work, and then creates a number of
tasks (threads) that can be scheduled and run by the operating system
concurrently.
- Each thread has local data, but also, shares the entire resources of
a.out. This saves the overhead associated with replicating a
program's resources for each thread. Each thread also benefits from a global
memory view because it shares the memory space of a.out.
- A thread's work may best be described as a subroutine within the main
program. Any thread can execute any subroutine at the same time as other
threads.
- Threads communicate with each other through global memory (updating
address locations). This requires synchronization constructs to insure that
more than one thread is not updating the same global address at any time.
- Threads can come and go, but a.out remains present to provide
the necessary shared resources until the application has completed.
- Threads are commonly associated with shared memory architectures and
operating systems.
 Implementations:
Implementations:
| Parallel Programming
Models |
Message Passing Model
- The message passing model demonstrates the following characteristics:
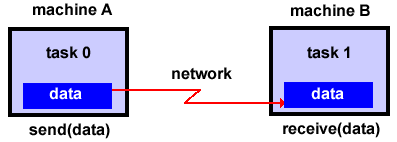
- A set of tasks that use their own local memory during computation.
Multiple tasks can reside on the same physical machine as well across an
arbitrary number of machines.
- Tasks exchange data through communications by sending and receiving
messages.
- Data transfer usually requires cooperative operations to be performed by
each process. For example, a send operation must have a matching receive
operation.
 Implementations:
Implementations:
- From a programming perspective, message passing implementations commonly
comprise a library of subroutines that are imbedded in source code. The
programmer is responsible for determining all parallelism.
- Historically, a variety of message passing libraries have been available
since the 1980s. These implementations differed substantially from each other
making it difficult for programmers to develop portable applications.
- In 1992, the MPI Forum was formed with the primary goal of establishing a
standard interface for message passing implementations.
- Part 1 of the Message Passing Interface (MPI) was released in 1994.
Part 2 (MPI-2) was released in 1996. Both MPI specifications are available on
the web at www.mcs.anl.gov/Projects/mpi/standard.html.
- MPI is now the "de facto" industry standard for message passing, replacing
virtually all other message passing implementations used for production work.
Most, if not all of the popular parallel computing platforms offer at least
one implementation of MPI. Very few have a full implementation of MPI-2.
- For shared memory architectures, MPI implementations usually don't use a
network for task communications. Instead, they use shared memory (memory
copies) for performance reasons.
| Parallel Programming
Models |
Data Parallel Model
- The data parallel model demonstrates the following characteristics:
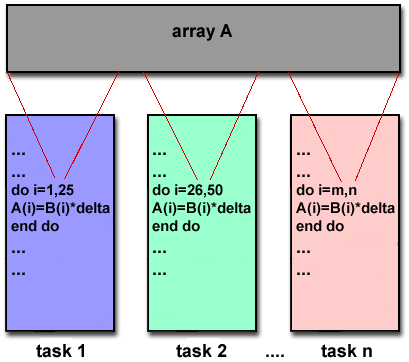
- Most of the parallel work focuses on performing operations on a data
set. The data set is typically organized into a common structure, such as an
array or cube.
- A set of tasks work collectively on the same data structure, however,
each task works on a different partition of the same data structure.
- Tasks perform the same operation on their partition of work, for
example, "add 4 to every array element".
- On shared memory architectures, all tasks may have access to the data
structure through global memory. On distributed memory architectures the data
structure is split up and resides as "chunks" in the local memory of each
task.
 Implementations:
Implementations:
| Parallel Programming
Models |
Other Models
- Other parallel programming models besides those previously mentioned
certainly exist, and will continue to evolve along with the ever changing
world of computer hardware and software. Only three of the more common ones
are mentioned here.
 Hybrid:
Hybrid:
- In this model, any two or more parallel programming models are combined.
- Currently, a common example of a hybrid model is the combination of the
message passing model (MPI) with either the threads model (POSIX threads) or
the shared memory model (OpenMP). This hybrid model lends itself well to the
increasingly common hardware environment of networked SMP machines.
- Another common example of a hybrid model is combining data parallel with
message passing. As mentioned in the data parallel model section previously,
data parallel implementations (F90, HPF) on distributed memory architectures
actually use message passing to transmit data between tasks, transparently to
the programmer.
 Single Program Multiple Data (SPMD):
Single Program Multiple Data (SPMD):
- SPMD is actually a "high level" programming model that can be built upon
any combination of the previously mentioned parallel programming models.
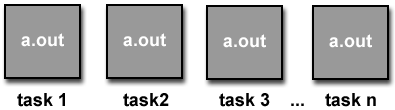
- A single program is executed by all tasks simultaneously.
- At any moment in time, tasks can be executing the same or different
instructions within the same program.
- SPMD programs usually have the necessary logic programmed into them to
allow different tasks to branch or conditionally execute only those parts of
the program they are designed to execute. That is, tasks do not necessarily
have to execute the entire program - perhaps only a portion of it.
- All tasks may use different data
 Multiple Program Multiple Data (MPMD):
Multiple Program Multiple Data (MPMD):
- Like SPMD, MPMD is actually a "high level" programming model that can be
built upon any combination of the previously mentioned parallel programming
models.
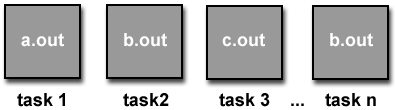
- MPMD applications typically have multiple executable object files
(programs). While the application is being run in parallel, each task can be
executing the same or different program as other tasks.
- All tasks may use different data
| Designing Parallel
Programs |
Automatic vs. Manual Parallelization
- Designing and developing parallel programs has characteristically been a
very manual process. The programmer is typically responsible for both
identifying and actually implementing parallelism.
- Very often, manually developing parallel codes is a time consuming,
complex, error-prone and iterative process.
- For a number of years now, various tools have been available to assist the
programmer with converting serial programs into parallel programs. The most
common type of tool used to automatically parallelize a serial program is a
parallelizing compiler or pre-processor.
- A parallelizing compiler generally works in two different ways:
- Fully Automatic
- The compiler analyzes the source code and identifies opportunities for
parallelism.
- The analysis includes identifying inhibitors to parallelism and
possibly a cost weighting on whether or not the parallelism would actually
improve performance.
- Loops (do, for) loops are the most frequent target for automatic
parallelization.
- Programmer Directed
- Using "compiler directives" or possibly compiler flags, the programmer
explicitly tells the compiler how to parallelize the code.
- May be able to be used in conjunction with some degree of automatic
parallelization also.
- If you are beginning with an existing serial code and have time or budget
constraints, then automatic parallelization may be the answer. However, there
are several important caveats that apply to automatic parallelization:
- Wrong results may be produced
- Performance may actually degrade
- Much less flexible than manual parallelization
- Limited to a subset (mostly loops) of code
- May actually not parallelize code if the analysis suggests there are
inhibitors or the code is too complex
- Most automatic parallelization tools are for Fortran
- The remainder of this section applies to the manual method of developing
parallel codes.
| Designing Parallel
Programs |
Understand the Problem and the Program
- Undoubtedly, the first step in developing parallel software is to first
understand the problem that you wish to solve in parallel. If you are starting
with a serial program, this necessitates understanding the existing code also.
- Before spending time in an attempt to develop a parallel solution for a
problem, determine whether or not the problem is one that can actually be
parallelized.
- Example of Parallelizable Problem:
| Calculate the potential energy for each of several thousand
independent conformations of a molecule. When done, find the minimum
energy conformation. |
This problem is able to be solved in parallel. Each of the molecular
conformations is independently determinable. The calculation of the minimum
energy conformation is also a parallelizable problem.
- Example of a Non-parallelizable Problem:
Calculation of the Fibonacci series (1,1,2,3,5,8,13,21,...) by use
of the formula: F(k + 2) = F(k + 1) + F(k) |
This is a non-parallelizable problem because the calculation of the
Fibonacci sequence as shown would entail dependent calculations rather than
independent ones. The calculation of the k + 2 value uses those of both k +
1 and k. These three terms cannot be calculated independently and therefore,
not in parallel.
- Identify the program's hotspots:
- Know where most of the real work is being done. The majority of
scientific and technical programs usually accomplish most of their work in a
few places.
- Profilers and performance analysis tools can help here
- Focus on parallelizing the hotspots and ignore those sections of the
program that account for little CPU usage.
- Identify bottlenecks in the program
- Are there areas that are disproportionately slow, or cause
parallelizable work to halt or be deferred? For example, I/O is usually
something that slows a program down.
- May be possible to restructure the program or use a different algorithm
to reduce or eliminate unnecessary slow areas
- Identify inhibitors to parallelism. One common class of inhibitor is
data dependence, as demonstrated by the Fibonacci sequence above.
- Investigate other algorithms if possible. This may be the single most
important consideration when designing a parallel application.
| Designing Parallel
Programs |
Partitioning
- One of the first steps in designing a parallel program is to break the
problem into discreet "chunks" of work that can be distributed to multiple
tasks. This is known as decomposition or partitioning.
- There are two basic ways to partition computational work among parallel
tasks: domain decomposition and functional
decomposition.
 Domain Decomposition:
Domain Decomposition:
- In this type of partitioning, the data associated with a problem is
decomposed. Each parallel task then works on a portion of of the data.
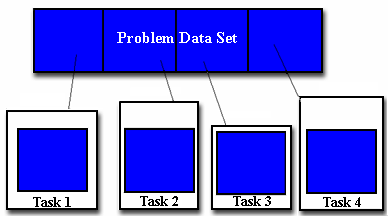
- There are different ways to partition data:

 Functional Decomposition:
Functional Decomposition:
- In this approach, the focus is on the computation that is to be performed
rather than on the data manipulated by the computation. The problem is
decomposed according to the work that must be done. Each task then performs a
portion of the overall work.
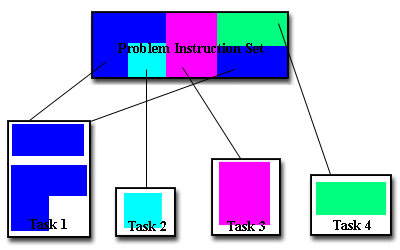
- Functional decomposition lends itself well to problems that can be split
into different tasks. For example:
- Ecosystem Modeling - This diagram shows five processes, each
running a different program. Each program calculates the population of a
given group, where each group's growth depends on that of its neighbors. As
time progresses, each process calculates its current state, then exchanges
information with the neighbor populations. All tasks then progress to
calculate the state at the next time step.
- Signal Processing - An audio signal data set is passed through
three distinct computational filters. Each filter is a separate process. The
first segment of data must pass through the first filter before progressing
to the second. When it does, the second segment of data passes through the
first filter. By the time the third segment of data is in the first filter,
all three tasks are busy.
- Climate Modeling - Each model component can be thought of as a
separate task. Arrows represent exchanges of data between components during
computation: the atmosphere model generates wind velocity data that are used
by the ocean model, the ocean model generates sea surface temperature data
that are used by the atmosphere model, and so on.
- Combining these two types of problem decomposition is common and natural.
| Designing Parallel
Programs |
Communications
 Who Needs Communications?
Who Needs Communications?
 Factors to Consider:
Factors to Consider:
There are a number of important factors to consider when designing your
program's inter-task communications:
- Cost of communications
- Inter-task communication virtually always implies overhead.
- Machine cycles and resources that could be used for computation are
instead used to package and transmit data.
- Communications frequently require some type of synchronization between
tasks, which can result in tasks spending time "waiting" instead of doing
work.
- Competing communication traffic can saturate the available network
bandwidth, further aggravating performance problems.
- Latency vs. Bandwidth
- latency is the time it takes to send a minimal (0 byte)
message from point A to point B. Commonly expressed as microseconds.
- bandwidth is the amount of data that can be communicated
per unit of time. Commonly expressed as megabytes/sec.
- Sending many small messages can cause latency to dominate communication
overheads. Often it is more efficient to package small messages into a
larger message, thus increasing the effective communications bandwidth.
- Visibility of communications
- With the Message Passing Model, communications are explicit and
generally quite visible and under the control of the programmer.
- With the Data Parallel Model, communications often occur transparently
to the programmer, particularly on distributed memory architectures. The
programmer may not even be able to know exactly how inter-task
communications are being accomplished.
- Synchronous vs. asynchronous communications
- Synchronous communications require some type of "handshaking" between
tasks that are sharing data. This can be explicitly structured in code by
the programmer, or it may happen at a lower level unknown to the programmer.
- Synchronous communications are often referred to as
blocking communications since other work must wait until the
communications have completed.
- Asynchronous communications allow tasks to transfer data independently
from one another. For example, task 1 can prepare and send a message to task
2, and then immediately begin doing other work. When task 2 actually
receives the data doesn't matter.
- Asynchronous communications are often referred to as
non-blocking communications since other work can be done while
the communications are taking place.
- Interleaving computation with communication is the single greatest
benefit for using asynchronous communications.
- Scope of communications
- Knowing which tasks must communicate with each other is critical during
the design stage of a parallel code. Both of the two scopings described
below can be implemented synchronously or asynchronously.
- Point-to-point - involves two tasks with one task acting
as the sender/producer of data, and the other acting as the
receiver/consumer.
- Collective - involves data sharing between more than two
tasks, which are often specified as being members in a common group, or
collective. Some common variations (there are more):
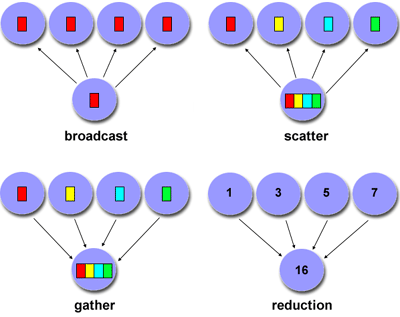
- Efficiency of communications
- Very often, the programmer will have a choice with regard to factors
that can affect communications performance. Only a few are mentioned here.
- Which implementation for a given model should be used? Using the Message
Passing Model as an example, one MPI implementation may be faster on a given
hardware platform than another.
- What type of communication operations should be used? As mentioned
previously, asynchronous communication operations can improve overall
program performance.
- Network media - some platforms may offer more than one network for
communications. Which one is best?
- Overhead and Complexity
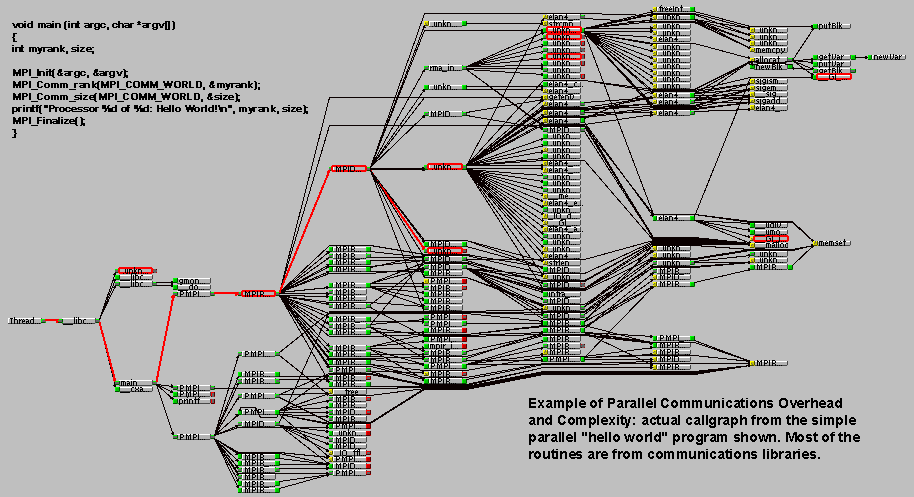
- Finally, realize that this is only a partial list of things to consider!!!
| Designing Parallel
Programs |
Synchronization
 Types of Synchronization:
Types of Synchronization:
- Barrier
- Usually implies that all tasks are involved
- Each task performs its work until it reaches the barrier. It then stops,
or "blocks".
- When the last task reaches the barrier, all tasks are synchronized.
- What happens from here varies. Often, a serial section of work must be
done. In other cases, the tasks are automatically released to continue their
work.
- Lock / semaphore
- Can involve any number of tasks
- Typically used to serialize (protect) access to global data or a section
of code. Only one task at a time may use (own) the lock / semaphore / flag.
- The first task to acquire the lock "sets" it. This task can then safely
(serially) access the protected data or code.
- Other tasks can attempt to acquire the lock but must wait until the task
that owns the lock releases it.
- Can be blocking or non-blocking
- Synchronous communication operations
- Involves only those tasks executing a communication operation
- When a task performs a communication operation, some form of
coordination is required with the other task(s) participating in the
communication. For example, before a task can perform a send operation, it
must first receive an acknowledgment from the receiving task that it is OK
to send.
- Discussed previously in the Communications section.
| Designing Parallel
Programs |
Data Dependencies
 Definition:
Definition:
- A dependence exists between program statements when the
order of statement execution affects the results of the program.
- A data dependence results from multiple use of the same
location(s) in storage by different tasks.
- Dependencies are important to parallel programming because they are one of
the primary inhibitors to parallelism.
 Examples:
Examples:
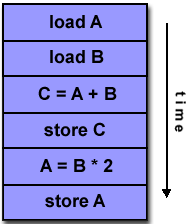
- Loop carried data dependence
DO 500 J = MYSTART,MYEND
A(J) = A(J-1) * 2.0
500 CONTINUE
|
The value of A(J-1) must be computed before the value of A(J), therefore
A(J) exhibits a data dependency on A(J-1). Parallelism is inhibited.
If Task 2 has A(J) and task 1 has A(J-1), computing the correct value of
A(J) necessitates:
- Distributed memory architecture - task 2 must obtain the value of A(J-1)
from task 1 after task 1 finishes its computation
- Shared memory architecture - task 2 must read A(J-1) after task 1
updates it
- Loop independent data dependence
task 1 task 2
------ ------
X = 2 X = 4
. .
. .
Y = X**2 Y = X**3
|
As with the previous example, parallelism is inhibited. The value of Y is
dependent on:
- Distributed memory architecture - if or when the value of X is
communicated between the tasks.
- Shared memory architecture - which task last stores the value of X.
- Although all data dependencies are important to identify when designing
parallel programs, loop carried dependencies are particularly important since
loops are possibly the most common target of parallelization efforts.
 How to Handle Data Dependencies:
How to Handle Data Dependencies:
- Distributed memory architectures - communicate required data at
synchronization points.
- Shared memory architectures -synchronize read/write operations between
tasks.
| Designing Parallel
Programs |
Load Balancing
- Load balancing refers to the practice of distributing work among tasks so
that all tasks are kept busy all of the time. It
can be considered a minimization of task idle time.
- Load balancing is important to parallel programs for performance reasons.
For example, if all tasks are subject to a barrier synchronization point, the
slowest task will determine the overall performance.
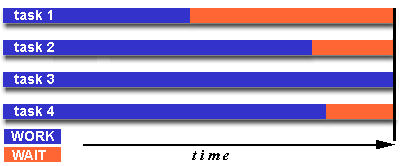
 How to Achieve Load Balance:
How to Achieve Load Balance:
- Equally partition the work each task receives
- For array/matrix operations where each task performs similar work,
evenly distribute the data set among the tasks.
- For loop iterations where the work done in each iteration is similar,
evenly distribute the iterations across the tasks.
- If a heterogeneous mix of machines with varying performance
characteristics are being used, be sure to use some type of performance
analysis tool to detect any load imbalances. Adjust work accordingly.
- Use dynamic work assignment
- Certain classes of problems result in load imbalances even if data is
evenly distributed among tasks:
- Sparse arrays - some tasks will have actual data to work on while
others have mostly "zeros".
- Adaptive grid methods - some tasks may need to refine their mesh while
others don't.
- N-body simulations - where some particles may migrate to/from
their original task domain to another task's; where the particles owned by
some tasks require more work than those owned by other tasks.
- When the amount of work each task will perform is intentionally
variable, or is unable to be predicted, it may be helpful to use a
scheduler - task pool approach. As each task finishes its
work, it queues to get a new piece of work.
- It may become necessary to design an algorithm which detects and handles
load imbalances as they occur dynamically within the code.
| Designing Parallel
Programs |
Granularity
 Computation / Communication Ratio:
Computation / Communication Ratio:
- In parallel computing, granularity is a qualitative measure of the ratio
of computation to communication.
- Periods of computation are typically separated from periods of
communication by synchronization events.
 Fine-grain Parallelism:
Fine-grain Parallelism: 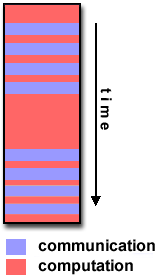
- Relatively small amounts of computational work are done between
communication events
- Low computation to communication ratio
- Facilitates load balancing
- Implies high communication overhead and less opportunity for performance
enhancement
- If granularity is too fine it is possible that the overhead required for
communications and synchronization between tasks takes longer than the
computation.
 Coarse-grain Parallelism:
Coarse-grain Parallelism: 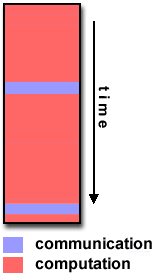
- Relatively large amounts of computational work are done between
communication/synchronization events
- High computation to communication ratio
- Implies more opportunity for performance increase
- Harder to load balance efficiently
 Which is Best?
Which is Best?
- The most efficient granularity is dependent on the algorithm and the
hardware environment in which it runs.
- In most cases the overhead associated with communications and
synchronization is high relative to execution speed so it is advantageous to
have coarse granularity.
- Fine-grain parallelism can help reduce overheads due to load imbalance.
| Designing Parallel
Programs |
I/O
 The Bad News:
The Bad News:
- I/O operations are generally regarded as inhibitors to parallelism
- Parallel I/O systems are immature or not available for all platforms
- In an environment where all tasks see the same filespace, write operations
will result in file overwriting
- Read operations will be affected by the fileserver's ability to handle
multiple read requests at the same time
- I/O that must be conducted over the network (NFS, non-local) can cause
severe bottlenecks
 The Good News:
The Good News:
- Some parallel file systems are available. For example:
- GPFS: General Parallel File System for AIX (IBM)
- Lustre: for Linux clusters (Cluster File Systems, Inc.)
- PVFS/PVFS2: Parallel Virtual File System for Linux clusters
(Clemson/Argonne/Ohio State/others)
- PanFS: Panasas ActiveScale File System for Linux clusters (Panasas,
Inc.)
- HP SFS: HP StorageWorks Scalable File Share. Lustre based parallel file
system (Global File System for Linux) product from HP
- The parallel I/O programming interface specification for MPI has been
available since 1996 as part of MPI-2. Vendor and "free" implementations are
now commonly available.
- Some options:
- If you have access to a parallel file system, investigate using it. If
you don't, keep reading...
- Rule #1: Reduce overall I/O as much as possible
- Confine I/O to specific serial portions of the job, and then use
parallel communications to distribute data to parallel tasks. For example,
Task 1 could read an input file and then communicate required data to other
tasks. Likewise, Task 1 could perform write operation after receiving
required data from all other tasks.
- For distributed memory systems with shared filespace, perform I/O in
local, non-shared filespace. For example, each processor may have /tmp
filespace which can used. This is usually much more efficient than
performing I/O over the network to one's home directory.
- Create unique filenames for each tasks' input/output file(s)
| Designing Parallel
Programs |
Limits and Costs of Parallel Programming
 Amdahl's Law:
Amdahl's Law:
- Amdahl's Law states that potential program speedup is defined by
the fraction of code (P) that can be parallelized:
1
speedup = --------
1 - P
|
- If none of the code can be parallelized, P = 0 and the speedup = 1 (no
speedup). If all of the code is parallelized, P = 1 and the speedup is
infinite (in theory).
If 50% of the code can be parallelized, maximum speedup = 2, meaning the
code will run twice as fast.
- Introducing the number of processors performing the parallel fraction of
work, the relationship can be modeled by:
1
speedup = ------------
P + S
---
N
|
where P = parallel fraction, N = number of processors and S = serial
fraction.
- It soon becomes obvious that there are limits to the scalability of
parallelism. For example, at P = .50, .90 and .99 (50%, 90% and 99% of the
code is parallelizable):
speedup
--------------------------------
N P = .50 P = .90 P = .99
----- ------- ------- -------
10 1.82 5.26 9.17
100 1.98 9.17 50.25
1000 1.99 9.91 90.99
10000 1.99 9.91 99.02
|
- However, certain problems demonstrate increased performance by increasing
the problem size. For example:
2D Grid Calculations 85 seconds 85%
Serial fraction 15 seconds 15%
We can increase the problem size by doubling the grid dimensions and
halving the time step. This results in four times the number of grid points
and twice the number of time steps. The timings then look like:
2D Grid Calculations 680 seconds 97.84%
Serial fraction 15 seconds 2.16%
- Problems that increase the percentage of parallel time with their size are
more scalable than problems with a fixed percentage of parallel
time.
 Complexity:
Complexity:
- In general, parallel applications are much more complex than corresponding
serial applications, perhaps an order of magnitude. Not only do you have
multiple instruction streams executing at the same time, but you also have
data flowing between them.
- The costs of complexity are measured in programmer time in virtually every
aspect of the software development cycle:
- Design
- Coding
- Debugging
- Tuning
- Maintenance
- Adhering to "good" software development practices is essential when when
working with parallel applications - especially if somebody besides you will
have to work with the software.
 Portability:
Portability:
- Thanks to standardization in several APIs, such as MPI, POSIX threads, HPF
and OpenMP, portability issues with parallel programs are not as serious as in
years past. However...
- All of the usual portability issues associated with serial programs apply
to parallel programs. For example, if you use vendor "enhancements" to
Fortran, C or C++, portability will be a problem.
- Even though standards exist for several APIs, implementations will differ
in a number of details, sometimes to the point of requiring code modifications
in order to effect portability.
- Operating systems can play a key role in code portability issues.
- Hardware architectures are characteristically highly variable and can
affect portability.
 Resource Requirements:
Resource Requirements:
- The primary intent of parallel programming is to decrease execution wall
clock time, however in order to accomplish this, more CPU time is required.
For example, a parallel code that runs in 1 hour on 8 processors actually uses
8 hours of CPU time.
- The amount of memory required can be greater for parallel codes than
serial codes, due to the need to replicate data and for overheads associated
with parallel support libraries and subsystems.
- For short running parallel programs, there can actually be a decrease in
performance compared to a similar serial implementation. The overhead costs
associated with setting up the parallel environment, task creation,
communications and task termination can comprise a significant portion of the
total execution time for short runs.
 Scalability:
Scalability:
- The ability of a parallel program's performance to scale is a result of a
number of interrelated factors. Simply adding more machines is rarely the
answer.
- The algorithm may have inherent limits to scalability. At some point,
adding more resources causes performance to decrease. Most parallel solutions
demonstrate this characteristic at some point.
- Hardware factors play a significant role in scalability. Examples:
- Memory-cpu bus bandwidth on an SMP machine
- Communications network bandwidth
- Amount of memory available on any given machine or set of machines
- Processor clock speed
- Parallel support libraries and subsystems software can limit scalability
independent of your application.
| Designing Parallel
Programs |
Performance Analysis and Tuning
- As with debugging, monitoring and analyzing parallel program execution is
significantly more of a challenge than for serial programs.
- A number of parallel tools for execution monitoring and program analysis
are available.
- Some are quite useful; some are cross-platform also.
- One starting point: Performance Analysis Tools Tutorial
- Work remains to be done, particularly in the area of scalability.
Array Processing
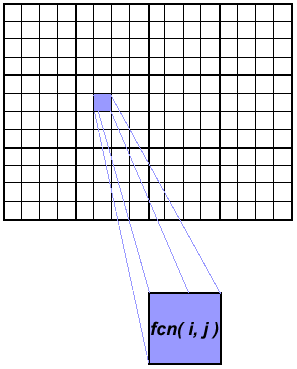
- This example demonstrates calculations on 2-dimensional array elements,
with the computation on each array element being independent from other array
elements.
- The serial program calculates one element at a time in sequential order.
- Serial code could be of the form:
do j = 1,n
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
|
- The calculation of elements is independent of one another - leads to an
embarrassingly parallel situation.
- The problem should be computationally intensive.
Array Processing
Parallel Solution 1
- Arrays elements are distributed so that each processor owns a portion of
an array (subarray).
- Independent calculation of array elements insures there is no need for
communication between tasks.
- Distribution scheme is chosen by other criteria, e.g. unit stride (stride
of 1) through the subarrays. Unit stride maximizes cache/memory usage.
- Since it is desirable to have unit stride through the subarrays, the
choice of a distribution scheme depends on the programming language. See the
Block
- Cyclic Distributions Diagram for the options.
- After the array is distributed, each task executes the portion of the loop
corresponding to the data it owns. For example, with Fortran block
distribution:
do j = mystart, myend
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
|
- Notice that only the outer loop variables are different from the serial
solution.
 One Possible Solution:
One Possible Solution:
- Implement as SPMD model.
- Master process initializes array, sends info to worker processes and
receives results.
- Worker process receives info, performs its share of computation and sends
results to master.
- Using the Fortran storage scheme, perform block distribution of the array.
- Pseudo code solution: red highlights changes
for parallelism.
find out if I am MASTER or WORKER
if I am MASTER
initialize the array
send each WORKER info on part of array it owns
send each WORKER its portion of initial array
receive from each WORKER results
else if I am WORKER
receive from MASTER info on part of array I own
receive from MASTER my portion of initial array
# calculate my portion of array
do j = my first column,my last column
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
send MASTER results
endif
|
Array Processing
Parallel Solution 2: Pool of Tasks
- The previous array solution demonstrated static load balancing:
- Each task has a fixed amount of work to do
- May be significant idle time for faster or more lightly loaded
processors - slowest tasks determines overall performance.
- Static load balancing is not usually a major concern if all tasks are
performing the same amount of work on identical machines.
- If you have a load balance problem (some tasks work faster than others),
you may benefit by using a "pool of tasks" scheme.
 Pool of Tasks Scheme:
Pool of Tasks Scheme:
 Discussion:
Discussion:
- In the above pool of tasks example, each task calculated an individual
array element as a job. The computation to communication ratio is finely
granular.
- Finely granular solutions incur more communication overhead in order to
reduce task idle time.
- A more optimal solution might be to distribute more work with each job.
The "right" amount of work is problem dependent.
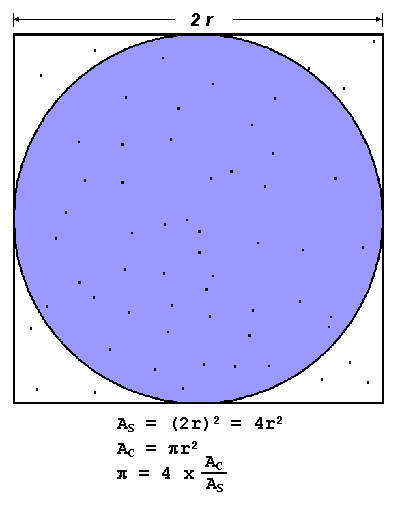
PI Calculation
- The value of PI can be calculated in a number of ways. Consider the
following method of approximating PI
- Inscribe a circle in a square
- Randomly generate points in the square
- Determine the number of points in the square that are also in the
circle
- Let r be the number of points in the circle divided by the number
of points in the square
- PI ~ 4 r
- Note that the more points generated, the better the approximation
- Serial pseudo code for this procedure:
npoints = 10000
circle_count = 0
do j = 1,npoints
generate 2 random numbers between 0 and 1
xcoordinate = random1 ; ycoordinate = random2
if (xcoordinate, ycoordinate) inside circle
then circle_count = circle_count + 1
end do
PI = 4.0*circle_count/npoints
|
|  |
Note that most of the time in running this program would be spent executing
the loop
Leads to an embarrassingly parallel solution
- Computationally intensive
- Minimal communication
- Minimal I/O
PI Calculation
Parallel Solution
- Parallel strategy: break the loop into portions that can be executed by
the tasks.
- For the task of approximating PI:
- Each task executes its portion of the loop a number of times.
- Each task can do its work without requiring any information from the
other tasks (there are no data dependencies).
- Uses the SPMD model. One task acts as master and collects the results.
- Pseudo code solution: red highlights changes
for parallelism.
npoints = 10000
circle_count = 0
p = number of tasks
num = npoints/p
find out if I am MASTER or WORKER
do j = 1,num
generate 2 random numbers between 0 and 1
xcoordinate = random1 ; ycoordinate = random2
if (xcoordinate, ycoordinate) inside circle
then circle_count = circle_count + 1
end do
if I am MASTER
receive from WORKERS their circle_counts
compute PI (use MASTER and WORKER calculations)
else if I am WORKER
send to MASTER circle_count
endif
|
Simple Heat Equation
- Most problems in parallel computing require communication among the
tasks. A number of common problems require communication with "neighbor"
tasks.
- The heat equation describes the temperature change over time, given
initial temperature distribution and boundary conditions.
- A finite differencing scheme is employed to solve the heat equation
numerically on a square region.
- The initial temperature is zero on the boundaries and high in the
middle.
- The boundary temperature is held at zero.
- For the fully explicit problem, a time stepping algorithm is used.
The elements of a 2-dimensional array represent the temperature at
points on the square.
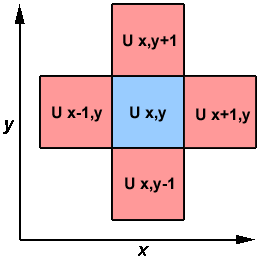
- The calculation of an element is dependent upon neighbor element
values.
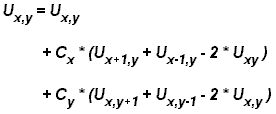
- A serial program would contain code like:
do iy = 2, ny - 1
do ix = 2, nx - 1
u2(ix, iy) =
u1(ix, iy) +
cx * (u1(ix+1,iy) + u1(ix-1,iy) - 2.*u1(ix,iy)) +
cy * (u1(ix,iy+1) + u1(ix,iy-1) - 2.*u1(ix,iy))
end do
end do
| |
  |
Simple Heat Equation
Parallel Solution 1
- Implement as an SPMD model
- The entire array is partitioned and distributed as subarrays to all tasks.
Each task owns a portion of the total array.
- Determine data dependencies
- Master process sends initial info to workers, checks for convergence and
collects results
- Worker process calculates solution, communicating as necessary with
neighbor processes
- Pseudo code solution: red highlights changes
for parallelism.
find out if I am MASTER or WORKER
if I am MASTER
initialize array
send each WORKER starting info and subarray
do until all WORKERS converge
gather from all WORKERS convergence data
broadcast to all WORKERS convergence signal
end do
receive results from each WORKER
else if I am WORKER
receive from MASTER starting info and subarray
do until solution converged
update time
send neighbors my border info
receive from neighbors their border info
update my portion of solution array
determine if my solution has converged
send MASTER convergence data
receive from MASTER convergence signal
end do
send MASTER results
endif
|
Simple Heat Equation
Parallel Solution 2: Overlapping Communication and
Computation
- In the previous solution, it was assumed that blocking communications were
used by the worker tasks. Blocking communications wait for the communication
process to complete before continuing to the next program instruction.
- In the previous solution, neighbor tasks communicated border data, then
each process updated its portion of the array.
- Computing times can often be reduced by using non-blocking communication.
Non-blocking communications allow work to be performed while communication is
in progress.
- Each task could update the interior of its part of the solution array
while the communication of border data is occurring, and update its border
after communication has completed.
- Pseudo code for the second solution: red
highlights changes for non-blocking communications.
find out if I am MASTER or WORKER
if I am MASTER
initialize array
send each WORKER starting info and subarray
do until all WORKERS converge
gather from all WORKERS convergence data
broadcast to all WORKERS convergence signal
end do
receive results from each WORKER
else if I am WORKER
receive from MASTER starting info and subarray
do until solution converged
update time
non-blocking send neighbors my border info
non-blocking receive neighbors border info
update interior of my portion of solution array
wait for non-blocking communication complete
update border of my portion of solution array
determine if my solution has converged
send MASTER convergence data
receive from MASTER convergence signal
end do
send MASTER results
endif
|
1-D Wave Equation
- In this example, the amplitude along a uniform, vibrating string is
calculated after a specified amount of time has elapsed.
- The calculation involves:
- the amplitude on the y axis
- i as the position index along the x axis
- node points imposed along the string
- update of the amplitude at discrete time steps.
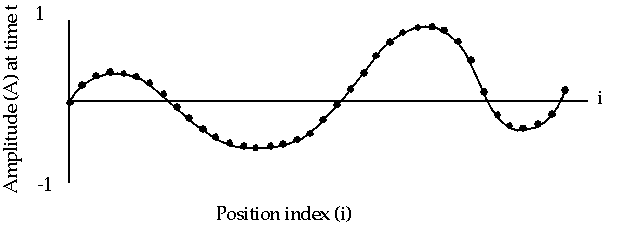
- The equation to be solved is the one-dimensional wave equation:
A(i,t+1) = (2.0 * A(i,t)) - A(i,t-1)
+ (c * (A(i-1,t) - (2.0 * A(i,t)) + A(i+1,t)))
where c is a constant
- Note that amplitude will depend on previous timesteps (t, t-1) and
neighboring points (i-1, i+1). Data dependence will mean that a parallel
solution will involve communications.
1-D Wave Equation
Parallel Solution
- Implement as an SPMD model
- The entire amplitude array is partitioned and distributed as subarrays to
all tasks. Each task owns a portion of the total array.
- Load balancing: all points require equal work, so the points should be
divided equally
- A block decomposition would have the work partitioned into the number of
tasks as chunks, allowing each task to own mostly contiguous data points.
- Communication need only occur on data borders. The larger the block size
the less the communication.
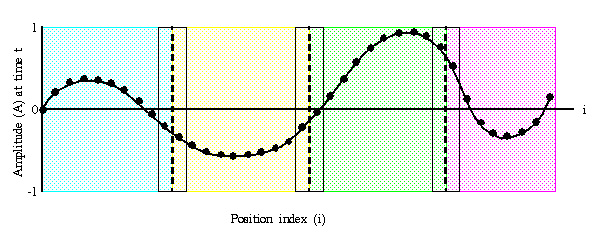
- Pseudo code solution:
find out number of tasks and task identities
#Identify left and right neighbors
left_neighbor = mytaskid - 1
right_neighbor = mytaskid +1
if mytaskid = first then left_neigbor = last
if mytaskid = last then right_neighbor = first
find out if I am MASTER or WORKER
if I am MASTER
initialize array
send each WORKER starting info and subarray
else if I am WORKER
receive starting info and subarray from MASTER
endif
#Update values for each point along string
#In this example the master participates in calculations
do t = 1, nsteps
send left endpoint to left neighbor
receive left endpoint from right neighbor
send right endpoint to right neighbor
receive right endpoint from left neighbor
#Update points along line
do i = 1, npoints
newval(i) = (2.0 * values(i)) - oldval(i)
+ (sqtau * (values(i-1) - (2.0 * values(i)) + values(i+1)))
end do
end do
#Collect results and write to file
if I am MASTER
receive results from each WORKER
write results to file
else if I am WORKER
send results to MASTER
endif
|
This completes the tutorial.
 |
Please complete the online evaluation form. |
Where would you like to go now?
| References and More
Information |
- Author: Blaise Barney, Livermore
Computing.
- A search on the WWW for "parallel programming" will yield a wide variety
of information.
- These materials were primarily developed from the following sources, some
of which are no longer maintained or available.
- Tutorials located in the Maui High Performance Computing Center's "SP
Parallel Programming Workshop".
- Tutorials located at the Cornell Theory Center's "Education and
Training" web page.
- "Designing and Building Parallel Programs". Ian Foster.